Travel Tips
Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Python数据分析实战——社会财富分配问题模拟二
在允许借贷情况下,研究以下问题
和初始模型的区别:
允许借贷意味着可以找亲友、银行、投资人借贷 → 资产为负时,仍然参与游戏
要求:
① 构建模型模拟,再次模拟财富分配情况
** 最富有的人相比于初始财富,翻了多少倍?
** 10%的人掌握着多少的财富?30%的人掌握着多少的财富?又有百分之多少人财富缩水至100元以下了?
② 绘制柱状图,查看该轮财富情况
** 横轴标签代表一个玩家的编号,柱子的高低变动反映该玩家财富值的变化
** 这里只需要每轮按照财富值排序绘制
** 前100轮,按照每10轮绘制一次柱状图,查看财富变化情况
** 100至1000轮,按照每100轮绘制一次柱状图,查看财富变化情况
** 1000至17000轮,按照每400轮绘制一次柱状图,查看财富变化情况
③ 游戏次数与财富分布的标准差的情况,绘图来表示
** 这里用允许借贷情况下模拟的结果
** 横坐标为游戏次数(总共17000次),纵坐标为财富分配标准差
** 绘制折线图
④ 玩家从18岁开始,在经过17年后为35岁,这个期间共进行游戏6200次左右,则此刻查看财富情况,将财富值为负的标记成“破产”,通过图表研究
该类玩家在今后的游戏中能否成功“逆袭”(财富值从负到正为逆袭)、
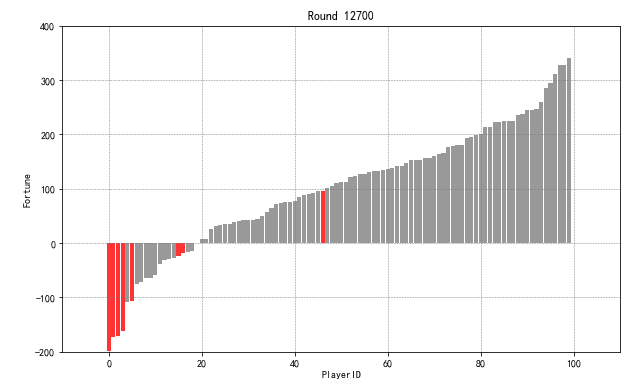
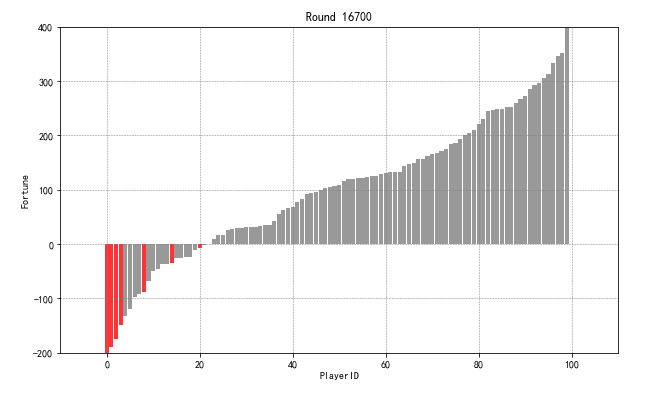
** 这里绘制柱状图 → 6200至17000轮,按照每500轮绘制一次柱状图
提示:
① 该模型只需要将初始模型中,“财富小于零时无需拿钱给别人”的条件删掉即可
② 最后绘制柱状图时,需要将负债的玩家标红,这里可以通过截取dataframe之后,给与color字段来设置颜色
# 这里注意:当某人的财富值降到0元时,他在该轮无需拿出1元钱给别人,但仍然有机会得到别人给出的钱
def game2(data, roundi):
round_i = pd.DataFrame({'pre_round':data[roundi-1],'lost':1}) # 设定每轮分配财富之前的情况
choice_i = pd.Series(np.random.choice(person_n,100))
gain_i = pd.DataFrame({'gain':choice_i.value_counts()}) # 这一轮中每个人随机指定给“谁”1元钱,并汇总这一轮每个人的盈利情况
round_i = round_i.join(gain_i)
round_i.fillna(0,inplace = True)
return round_i['pre_round'] - round_i['lost'] + round_i['gain']
# 合并数据,得到这一轮财富分配的结果
print('finished!')
person_n = [x for x in range(1,101)]
fortune = pd.DataFrame([100 for i in range(100)], index = person_n)
fortune.index.name = 'id'
# 设定初始参数:游戏玩家100人,起始资金100元
starttime = time.time() # 模型开始时间
for round in range(1,17001):
fortune[round] = game2(fortune,round) # 进行17000轮随机分配模拟
game2_result = fortune.T # 转置后得到结果数据 → 列为每一个人的id,行为每一轮的财富分配结果
endtime = time.time() # 模型结束时间
print('模型总共用时%i秒' % (endtime - starttime))
# 计算时间
game2_result.tail()
# 查看最后5条数据
round_17000_2 = pd.DataFrame({'money':game2_result.iloc[17000]}).sort_values(by = 'money',ascending = False).reset_index()
round_17000_2['fortune_pre'] = round_17000_2['money'] / round_17000_2['money'].sum()
round_17000_2['fortune_cumsum'] = round_17000_2['fortune_pre'].cumsum()
round_17000_2.head()
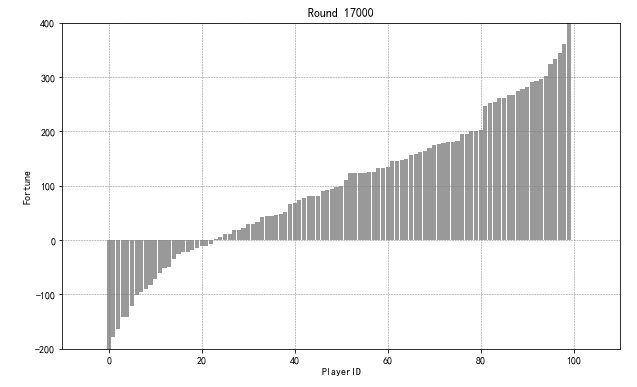
# 最后一轮中,最富有的人财富值为458元,相比于初始财富,翻了4.58倍
# 10%的人掌握着33%的财富,20%的人掌握着59%的财富?
# 50%的人财富缩水至100元以下了?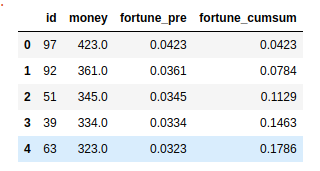
os.chdir('/home/zty/Documents/python/Python进阶数据分析及可视化/实战/练习08_社会财富分配问题模拟/财富分配模型_允许借贷/')
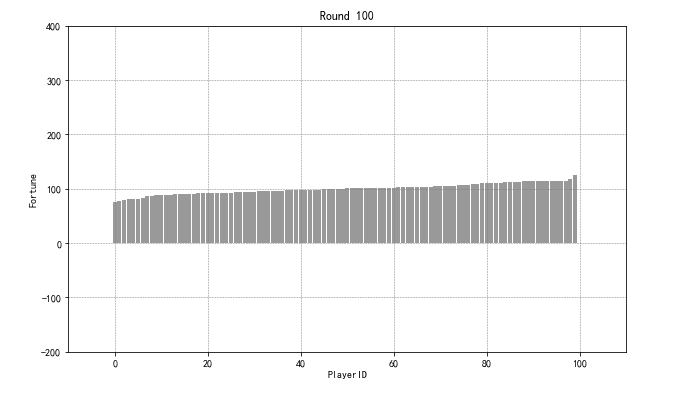
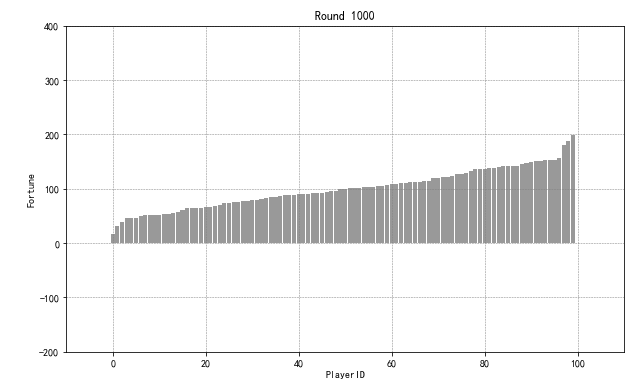
def graph3(data,start,end,length):
for n in list(range(start,end,length)):
datai = data.iloc[n].sort_values().reset_index()[n]
plt.figure(figsize = (10,6))
plt.bar(datai.index,datai.values,color='gray',alpha = 0.8,width = 0.9)
plt.grid(color='gray', linestyle='--', linewidth=0.5)
plt.ylim((-200,400))
plt.xlim((-10,110))
plt.title('Round %d' % n)
plt.xlabel('PlayerID')
plt.ylabel('Fortune')
plt.savefig('graph3_round_%d.png' % n, dpi=200)
# 创建绘图函数2
graph3(game2_result,0,100,10)
graph3(game2_result,100,1000,100)
graph3(game2_result,1000,17400,400)
print('finished!')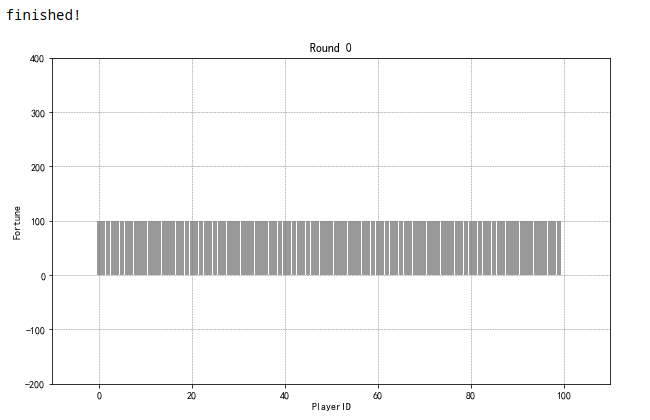
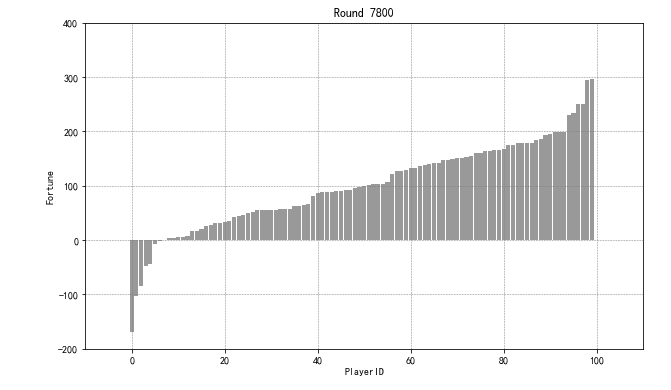

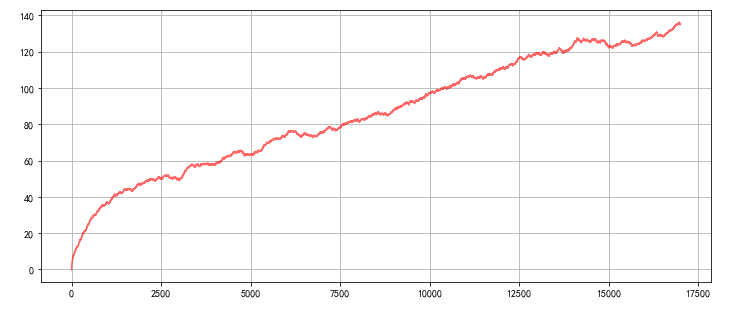
game2_st = game2_result.std(axis = 1) game2_st.plot(figsize = (12,5),color = 'red',alpha = 0.6,grid = True) plt.show() # 游戏早期前2000轮的标准差变动最为激烈; # 而在6000-6500轮游戏后,标准差的变化趋于平缓,但仍在上升; # 按照我们设定的游戏与人生的对应规则,这时玩家年龄为35岁
# 通过图表研究该类玩家在今后的游戏中能否成功“逆袭”(财富值从负到正为逆袭)、
# 这里绘制折线图
game2_round6200 = pd.DataFrame({'money':game2_result.iloc[6200].sort_values().reset_index()[6200],
'id':game2_result.iloc[6200].sort_values().reset_index()['id'],
'color':'gray'})
game2_round6200['color'][game2_round6200['money'] < 0] = 'red'
id_pc = game2_round6200['id'][game2_round6200['money'] < 0].tolist()
print('财富值为负的玩家id为:\n',id_pc)
# 筛选数据
# 设置颜色参数
plt.figure(figsize = (10,6))
plt.bar(game2_round6200.index,game2_round6200['money'],color = game2_round6200['color'],alpha = 0.8,width = 0.9)
plt.grid(color='gray', linestyle='--', linewidth=0.5)
plt.ylim((-200,400))
plt.xlim((-10,110))
plt.title('Round 6200')
plt.xlabel('PlayerID')
plt.ylabel('Fortune')
plt.show()
# 绘制柱状图
os.chdir('/home/zty/Documents/python/Python进阶数据分析及可视化/实战/练习08_社会财富分配问题模拟/财富分配模型_允许借贷_负债玩家逆袭/')
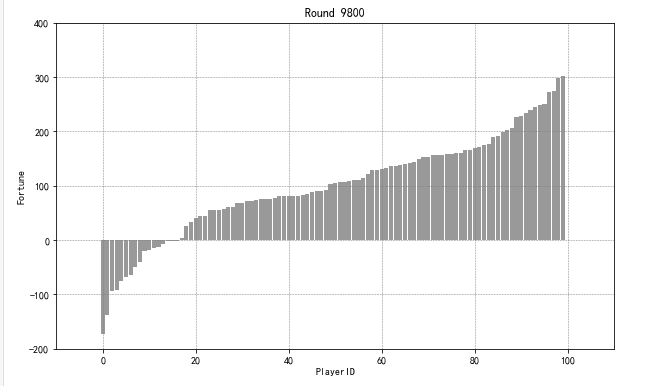
def graph4(data,start,end,length):
for n in list(range(start,end,length)):
datai = pd.DataFrame({'money':data.iloc[n],'color':'gray'})
datai['color'].loc[id_pc] = 'red'
datai = datai.sort_values(by = 'money').reset_index()
plt.figure(figsize = (10,6))
plt.bar(datai.index,datai['money'],color=datai['color'],alpha = 0.8,width = 0.9)
plt.grid(color='gray', linestyle='--', linewidth=0.5)
plt.ylim((-200,400))
plt.xlim((-10,110))
plt.title('Round %d' % n)
plt.xlabel('PlayerID')
plt.ylabel('Fortune')
plt.savefig('graph4_round_%d.png' % n, dpi=200)
# 创建绘图函数2
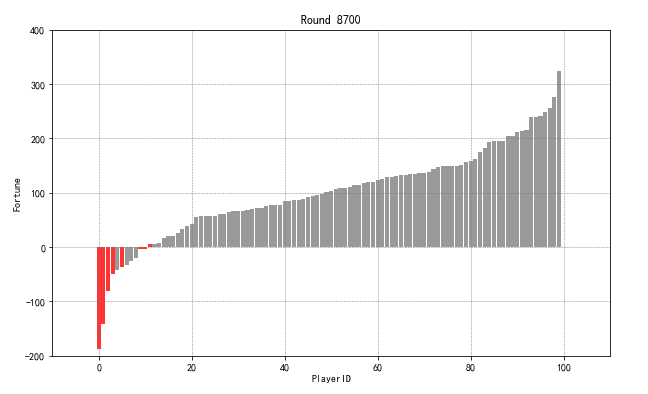
graph4(game2_result,6200,17000,500)
print('finished!')
# 结论
# 以35岁为界,虽然破产以后,不足一半的概率回复到普通人的生活,但想要逆袭暴富,却是相当困难的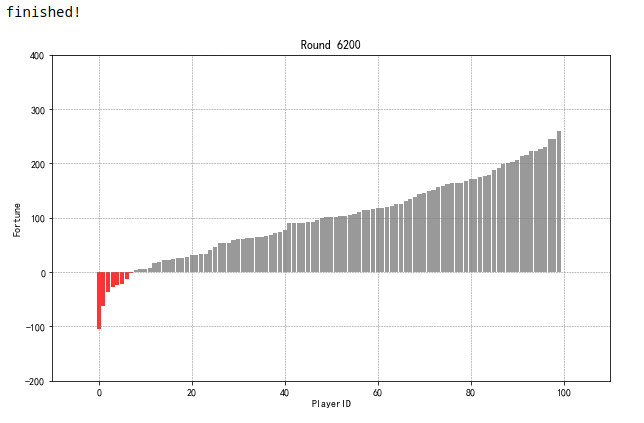

Sed ac lorem felis. Ut in odio lorem. Quisque magna dui, maximus ut commodo sed, vestibulum ac nibh. Aenean a tortor in sem tempus auctor
December 4, 2020 at 3:12 pm

Sed ac lorem felis. Ut in odio lorem. Quisque magna dui, maximus ut commodo sed, vestibulum ac nibh. Aenean a tortor in sem tempus auctor
December 4, 2020 at 3:12 pm

Donec in ullamcorper quam. Aenean vel nibh eu magna gravida fermentum. Praesent eget nisi pulvinar, sollicitudin eros vitae, tristique odio.
December 4, 2020 at 3:12 pm
我是 s enim interduante quis metus. Duis porta ornare nulla ut bibendum
Rosie
6 minutes ago